Matplotlib - Gráficos en Python#

Important

Para tener presente

El paquete para construir gráficos por excelencia en Python es Matplotlib, una de las librerías más usadas para crear todo tipo de visualizaciones.

¿Cómo funciona?#

Matplotlib grafica sus datos sobre una instancia llamada Figure, cada una de estas contendrá uno o más Axes (un área en la que los puntos tienen coordenadas). Usualmente se utiliza la interfaz pyplot basada en algunos estilos y comandos de MATLAB.

Veamos un sencillo ejemplo:

import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
fig, ax = plt.subplots()  # Creamos una figura con un sistema de ejes.
ax.plot([1, 2, 3, 4], [1, 4, 2, 3])  # Pintamos algunos datos.

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [1], in <cell line: 1>()
----> 1 import matplotlib.pyplot as plt
      2 import numpy as np
      3 get_ipython().run_line_magic('matplotlib', 'inline')

ModuleNotFoundError: No module named 'matplotlib'

Important

Para tener presente

IPython tiene un conjunto de “funciones mágicas” predefinidas a las que puede llamar con una sintaxis de estilo de línea de comandos. Hay dos tipos de magia, orientada a líneas y orientada a celdas.

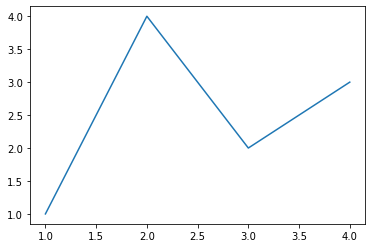
Sin necesidad de fijar los ejes de una figura podemos hacer el mismo gráfico:

plt.plot([1, 2, 3, 4], [1, 4, 2, 3]) 

[<matplotlib.lines.Line2D at 0x7f8cb9c88250>]

Partes de una figura#

Veamos los componentes de una figura de Matplotlib:

Tomado de https://matplotlib.org/3.2.2/tutorials/introductory/usage.html#sphx-glr-tutorials-introductory-usage-py

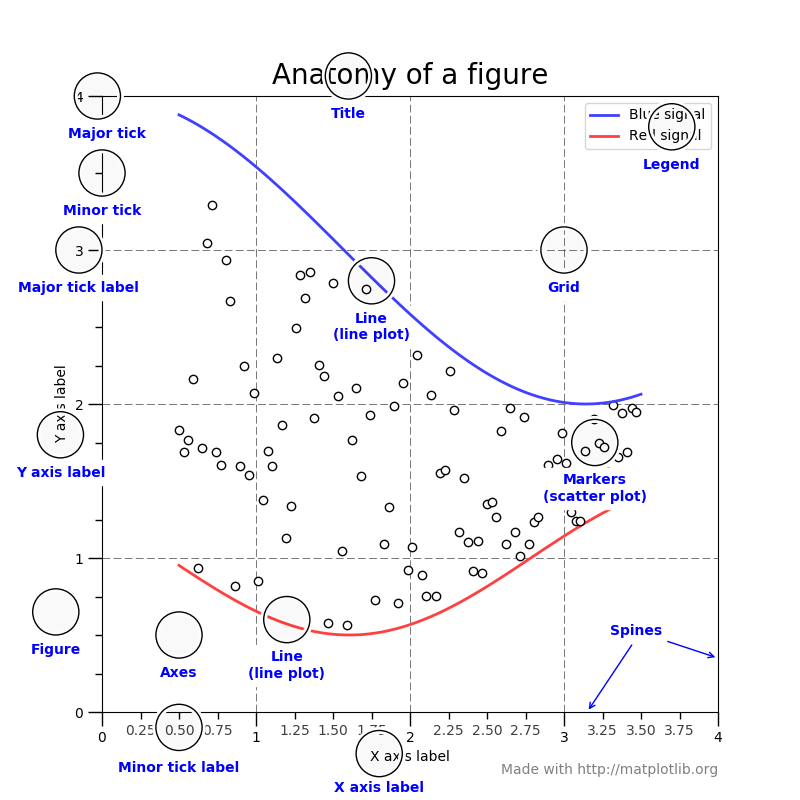
Sin necesidad de definir nuevas figuras veremos un ejemplo con algunos elementos descritos en la figura:

x=np.linspace(0, 10, 101)

np.sin(x)

array([ 0.        ,  0.09983342,  0.19866933,  0.29552021,  0.38941834,
        0.47942554,  0.56464247,  0.64421769,  0.71735609,  0.78332691,
        0.84147098,  0.89120736,  0.93203909,  0.96355819,  0.98544973,
        0.99749499,  0.9995736 ,  0.99166481,  0.97384763,  0.94630009,
        0.90929743,  0.86320937,  0.8084964 ,  0.74570521,  0.67546318,
        0.59847214,  0.51550137,  0.42737988,  0.33498815,  0.23924933,
        0.14112001,  0.04158066, -0.05837414, -0.15774569, -0.2555411 ,
       -0.35078323, -0.44252044, -0.52983614, -0.61185789, -0.68776616,
       -0.7568025 , -0.81827711, -0.87157577, -0.91616594, -0.95160207,
       -0.97753012, -0.993691  , -0.99992326, -0.99616461, -0.98245261,
       -0.95892427, -0.92581468, -0.88345466, -0.83226744, -0.77276449,
       -0.70554033, -0.63126664, -0.55068554, -0.46460218, -0.37387666,
       -0.2794155 , -0.1821625 , -0.0830894 ,  0.0168139 ,  0.1165492 ,
        0.21511999,  0.31154136,  0.40484992,  0.49411335,  0.57843976,
        0.6569866 ,  0.72896904,  0.79366786,  0.85043662,  0.8987081 ,
        0.93799998,  0.96791967,  0.98816823,  0.99854335,  0.99894134,
        0.98935825,  0.96988981,  0.94073056,  0.90217183,  0.85459891,
        0.79848711,  0.7343971 ,  0.66296923,  0.58491719,  0.50102086,
        0.41211849,  0.31909836,  0.22288991,  0.12445442,  0.02477543,
       -0.07515112, -0.17432678, -0.27176063, -0.36647913, -0.45753589,
       -0.54402111])

x = np.linspace(0, 10, 101)

plt.plot(x, np.sin(x),'r-', label='sin(x)')#1
plt.plot(x, np.cos(x), 'y-',label='cos(x)')#1
plt.legend()#2
plt.grid()#3
plt.title("Una figura simple")#4
plt.xlabel('Eje x')#5
plt.ylabel('Eje y')#6
plt.show()#7

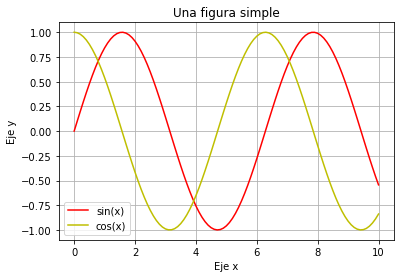
En el bloque de código anterior hemos agregado unos comentarios en forma de número para aclararlos en seguida: 1.

plt.plot(x, np.sin(x),'r-', label='sin(x)')

x los valores de éste argumento serán tenidos en cuenta para el eje horizontal. np.sin(x) son los valores resultantes de aplicar la función seno a cada elemento del arreglo x. 'r-' este argumento hace que la gráfica sea de color rojo y su trazo sea continuo. label='sin(x)' agrega a la leyenda ‘sin(x)’. 2. Hace que se “pinte” la leyenda sobre la gráfica. 3. Agrega la grilla a la gráfica. 4. Agrega el título a la gráfica. 5. Agrega el nombre del eje x. 6. Agrega el nombre del eje y. 7. Muestra la gráfica elaborada.

Podemos hacer un elemento interactivo con algunas de las funciones trigonométricas:

from ipywidgets import interact
from numpy import *

def graficadoradefuncionestrigonometricas(t):
    x=np.linspace(-10,10,500)
    y=eval(t)
    plt.plot(x,y,label=t)
    plt.legend()
    return

graficadoradefuncionestrigonometricas('sin(x)')

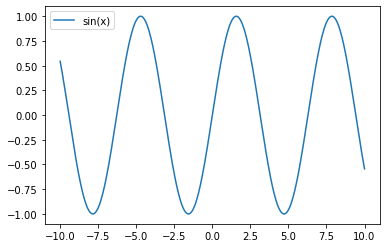
lista=["sin(x)","cos(x)","tan(x)"]

interact(graficadoradefuncionestrigonometricas,t=lista)

<function __main__.graficadoradefuncionestrigonometricas(t)>

Ejercicio#

Modifica el código anterior para que se grafiquen los monomios x, x^2, …, x^10.

Figura y ejes como variables#

Podemos usar instancias para expresar tanto a la figura como los ejes sobre la figura:

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot([1, 2, 3, 4], [10, 20, 25, 30], color='lightblue', linewidth=3)
ax.scatter([0.3, 3.8, 1.2, 2.5], [11, 25, 9, 26], color='darkgreen')
ax.set_xlim(-1, 6)
ax.set_ylim(6, 31)
plt.show()

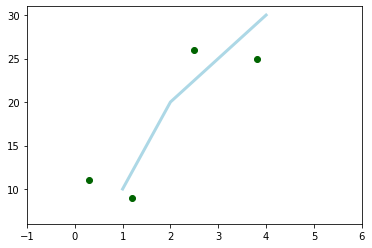
En este ejemplo utilizamos plt.figure() para definir la figura y fig.add_subplot(111) para crear la ‘zona de dibujo’.

En Matplotlib se puiede definir sobre una misma figura varias zonas de dibujo:

x=np.linspace(0,10,100)
fig = plt.figure(figsize=(20,20))

ax = fig.add_subplot(221)

ax.plot([1, 2, 3, 4], [10, 20, 25, 30], color='lightblue', linewidth=3,label="línea")
ax.scatter([0.3, 3.8, 1.2, 2.5], [11, 25, 9, 26], color='darkgreen', marker='^',label="marker")
ax.legend()
plt.title("Primera 'zona de dibujo'")

ax2 = fig.add_subplot(222)

ax2.plot(x, x, label='línea')
ax2.legend()
plt.title("Segunda 'zona de dibujo'")

ax3 = fig.add_subplot(223)
ax3.plot([1, 2, 3, 4], [10, 20, 25, 30], color='lightblue', linewidth=3,label="línea")
ax3.legend()
plt.title("Tercera 'zona de dibujo'")

ax4 = fig.add_subplot(224)
ax4.plot(x, x, label='línea')
ax4.legend()
plt.title("Cuarta 'zona de dibujo'")
plt.show()

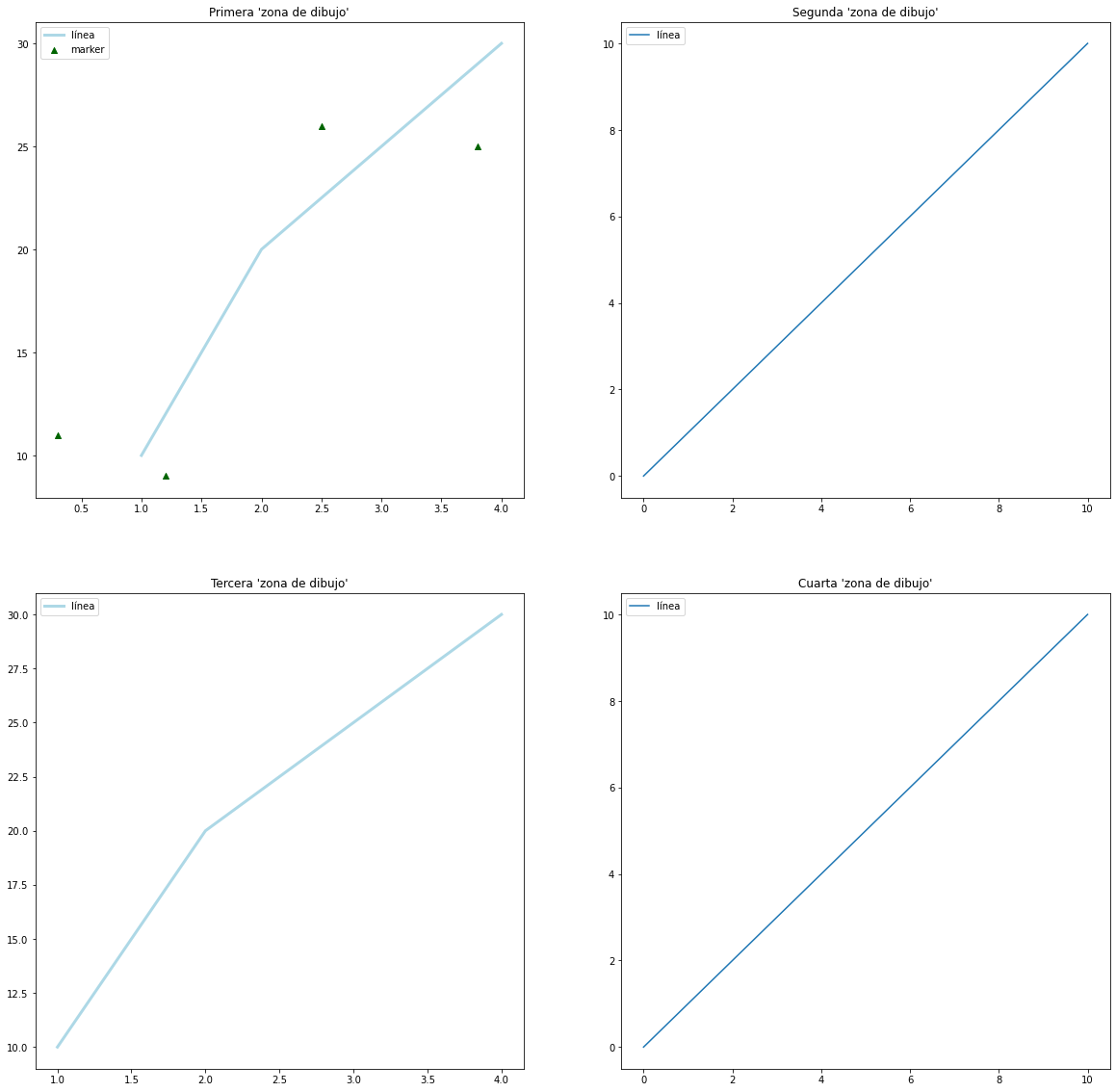
Las líneas que contienen fig.add_subplot(221) nos indican que las gráficas estarán distribuidas en una parrilla 2x2 y estamos modificando la primera de ellas.

Las zonas de dibujo (Axes) siempre deben vincularse a una Figura. Podemos fijar un título para cada zona usando set_title(). Por cada Axes tenemos 2 o tres ejes (Axis), entre sus funcioes útiles tenemos:

Para controlar el límite de los ejes:

axes.Axes.set_xlim()
axes.Axes.set_ylim()

Para fijar una etiqueta en el eje

set_xlabel()
set_ylabel()

Veamos un ejemplo:

fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(121)
ax.plot([1, 2, 3, 4], [10, 20, 25, 30], color='lightblue', linewidth=3,label="línea")
ax.scatter([0.3, 3.8, 1.2, 2.5], [11, 25, 9, 26], color='darkgreen', marker='^',label="marker")
ax.set_xlim(0, 4.5)
ax.set_ylim(0, 31)
ax.set_ylabel("Eje y")
ax.set_xlabel("Eje x")
ax.legend()
ax.set_title("Primera 'zona de dibujo'")
ax2 = fig.add_subplot(122)
ax2.plot(x, x, label='línea')
ax2.legend()
ax2.set_title("Segunda 'zona de dibujo'")
plt.show()

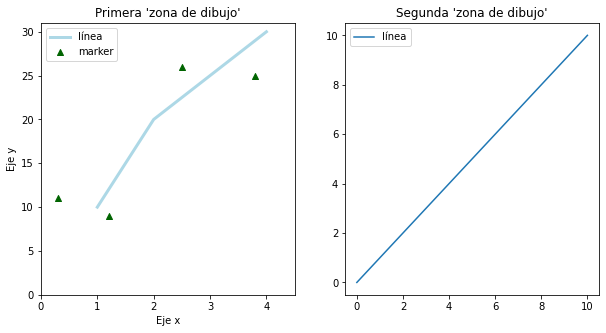
Diferentes tipos de gráficos#

Veamos ahora una galería de gráficos utilizados en diferentes contextos. Según los ejemplos anteriores tenemos la posibilidad de graficar puntos sobre el plano utilizando plt.plot()

El commando `plt.plot()`#

plt.plot([1,2,4,3,1,2,8,7])
plt.ylabel('Una lista de valores')
plt.show()

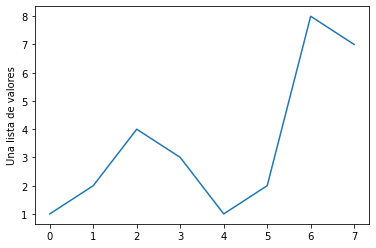
Notemos que el índice del valor aparece en el eje horizontal y el valor en el eje vertical.

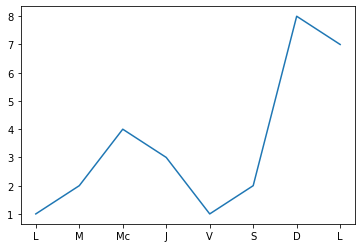
plt.plot([1,2,4,3,1,2,8,7])
plt.xticks(ticks=range(0,8),labels=['L','M','Mc','J','V','S','D','L'])
plt.show()

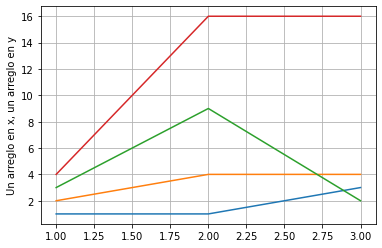
plt.plot([1,2,3],[[1,2,3,4], [1,4,9,16],[3,4,2,16]]) 
plt.ylabel('Un arreglo en x, un arreglo en y')
plt.grid()
plt.show()
#El 1 esta asociado con el 1,2,3 y 4
#El 2 con 1,4,9  y 16
#El 3 con 3,4,2 y 16

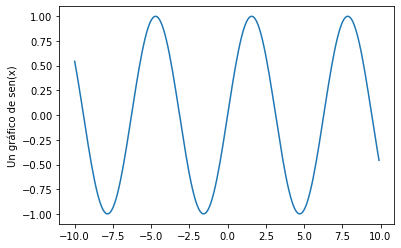
x=np.arange(-10,10,0.1)
y=np.sin(x)
plt.plot(x,y) 
plt.ylabel('Un gráfico de sen(x)')
plt.show()

No obstante podemos graficar sin unir los puntos:

#Gráfica de una lista de puntos:
plt.plot([1, 2, 3, 4], [1, 4, 9, 16], '^y')
plt.axis([0, 6, 0, 20])#ajuste de valores de los ejes
plt.show()

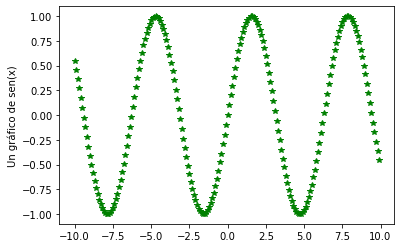
#Gráfico de una función aplicada a una lista
x=np.arange(-10,10,0.1)
y=np.sin(x)
plt.plot(x,y,'g*') 
plt.ylabel('Un gráfico de sen(x)')
plt.show()

Varias funciones en un mismo gráfico:

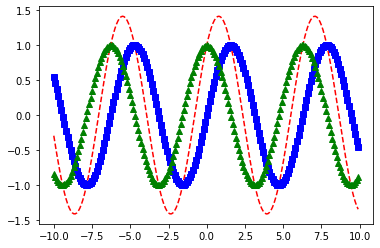
plt.plot(x,np.sin(x)+np.cos(x) , 'r--', x, np.sin(x), 'bs', x, np.cos(x), 'g^')
plt.show()

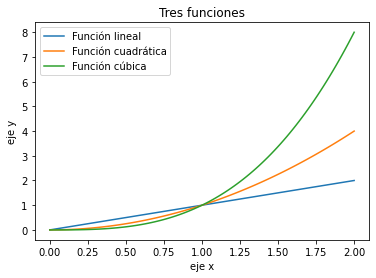
x = np.linspace(0, 2, 100)
fig, ax = plt.subplots()  # Creamos una instancia de figura y una zona de dibujo.
ax.plot(x, x, label='Función lineal')  #Agregamos función por función
ax.plot(x, x**2, label='Función cuadrática')  
ax.plot(x, x**3, label='Función cúbica') 
ax.set_xlabel('eje x') #Ajustamos títulos de ejes
ax.set_ylabel('eje y')  
ax.set_title("Tres funciones") #Ponemos título a la gráfica
ax.legend()  

<matplotlib.legend.Legend at 0x7f8cb8707a00>

¿Qué estilos podemos agregar a las líneas?#

Las líneas, como hemos visto, tienen muchas propiedades que podemos modificar, entre ellas están: el color, el tipo de trazado, el grosor, etc. Con las siguientes líneas de comando veremos otras propiedades y las posibles modificaciones a realizar:

line,=plt.plot([1,2,3])
plt.setp(line)

  agg_filter: a filter function, which takes a (m, n, 3) float array and a dpi value, and returns a (m, n, 3) array
  alpha: float or None
  animated: bool
  antialiased or aa: bool
  clip_box: `.Bbox`
  clip_on: bool
  clip_path: Patch or (Path, Transform) or None
  color or c: color
  contains: callable
  dash_capstyle: {'butt', 'round', 'projecting'}
  dash_joinstyle: {'miter', 'round', 'bevel'}
  dashes: sequence of floats (on/off ink in points) or (None, None)
  data: (2, N) array or two 1D arrays
  drawstyle or ds: {'default', 'steps', 'steps-pre', 'steps-mid', 'steps-post'}, default: 'default'
  figure: `.Figure`
  fillstyle: {'full', 'left', 'right', 'bottom', 'top', 'none'}
  gid: str
  in_layout: bool
  label: object
  linestyle or ls: {'-', '--', '-.', ':', '', (offset, on-off-seq), ...}
  linewidth or lw: float
  marker: marker style
  markeredgecolor or mec: color
  markeredgewidth or mew: float
  markerfacecolor or mfc: color
  markerfacecoloralt or mfcalt: color
  markersize or ms: float
  markevery: None or int or (int, int) or slice or List[int] or float or (float, float)
  path_effects: `.AbstractPathEffect`
  picker: float or callable[[Artist, Event], Tuple[bool, dict]]
  pickradius: float
  rasterized: bool or None
  sketch_params: (scale: float, length: float, randomness: float)
  snap: bool or None
  solid_capstyle: {'butt', 'round', 'projecting'}
  solid_joinstyle: {'miter', 'round', 'bevel'}
  transform: `matplotlib.transforms.Transform`
  url: str
  visible: bool
  xdata: 1D array
  ydata: 1D array
  zorder: float

Gráficos de dispersión#

Son gráficos en los que se grafican con coordenadas cartesianas los valores de dos variables en un conjunto de datos.

Para dar un buen ejemplo, iniciemos definiendo una base de datos aleatoria:

data={}
data = {'Eje x': np.arange(50),
        'Tamaño': np.random.randn(50),
        'Color': np.random.randint(0, 50, 50)}
data['Eje y'] = data['Eje x'] + 10 * np.random.randn(50)
data['Tamaño'] = np.abs(data['Tamaño']) * 100

import pandas as pd
data=pd.DataFrame(data)
data

	Eje x	Tamaño	Color	Eje y
0	0	70.550731	4	5.220343
1	1	3.670264	44	7.765722
2	2	120.810922	45	-4.461533
3	3	105.421219	8	-6.189932
4	4	189.665020	16	8.799888
5	5	61.625229	33	9.454881
6	6	10.192622	27	10.641279
7	7	16.537129	8	7.843916
8	8	10.938201	2	8.678060
9	9	85.018116	38	-8.682972
10	10	60.049978	49	11.568368
11	11	72.997189	18	14.371010
12	12	59.975775	29	-0.890044
13	13	131.915788	46	3.220360
14	14	11.906210	30	3.956789
15	15	68.841175	7	3.597548
16	16	134.416421	23	21.328567
17	17	123.530091	20	17.091576
18	18	103.000883	48	12.063169
19	19	68.952206	30	17.407299
20	20	44.824560	47	21.756066
21	21	2.480242	26	2.997751
22	22	105.977239	31	18.963290
23	23	44.501640	5	21.221243
24	24	24.592700	32	22.829913
25	25	99.021131	32	32.325663
26	26	50.512905	49	36.201611
27	27	100.035327	31	21.125156
28	28	204.973232	44	30.326489
29	29	74.880539	13	16.279830
30	30	156.925645	19	27.388052
31	31	104.996458	24	42.025137
32	32	212.310766	27	44.440880
33	33	118.668638	28	29.513454
34	34	34.736550	30	30.940591
35	35	60.804122	45	40.887989
36	36	17.902387	30	43.138015
37	37	29.991183	32	42.454406
38	38	1.383739	21	36.109898
39	39	48.206123	49	56.716654
40	40	84.587488	39	38.364313
41	41	4.828846	9	61.488268
42	42	186.199165	7	34.175242
43	43	38.688101	42	45.267664
44	44	29.886169	23	50.130008
45	45	48.845386	48	49.810560
46	46	87.989968	5	48.412401
47	47	99.015713	21	42.079851
48	48	8.882612	34	27.290519
49	49	228.308129	17	52.359274

data['Eje x']

    0
    1
    2
    3
    4
    5
    6
    7
    8
    9
  10
  11
  12
  13
  14
  15
  16
  17
  18
  19
  20
  21
  22
  23
  24
  25
  26
  27
  28
  29
  30
  31
  32
  33
  34
  35
  36
  37
  38
  39
  40
  41
  42
  43
  44
  45
  46
  47
  48
  49
Name: Eje x, dtype: int32

data['Eje y']

    5.220343
    7.765722
   -4.461533
   -6.189932
    8.799888
    9.454881
   10.641279
    7.843916
    8.678060
   -8.682972
  11.568368
  14.371010
  -0.890044
   3.220360
   3.956789
   3.597548
  21.328567
  17.091576
  12.063169
  17.407299
  21.756066
   2.997751
  18.963290
  21.221243
  22.829913
  32.325663
  36.201611
  21.125156
  30.326489
  16.279830
  27.388052
  42.025137
  44.440880
  29.513454
  30.940591
  40.887989
  43.138015
  42.454406
  36.109898
  56.716654
  38.364313
  61.488268
  34.175242
  45.267664
  50.130008
  49.810560
  48.412401
  42.079851
  27.290519
  52.359274
Name: Eje y, dtype: float64

plt.scatter('Eje x', 'Eje y',data=data)
plt.xlabel('Valores guardados en "Eje x"')
plt.ylabel('Valores guardados en "Eje y"')
plt.grid()
plt.show()

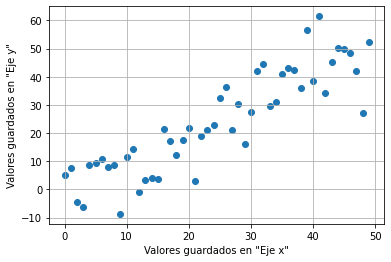
En los gráficos de dispersión, podemos agregar más variables al gráfico sin aumentar su dimensión. Introduzcamos una variable, el tamaño:

plt.scatter('Eje x', 'Eje y',s='Tamaño',data=data)#1
plt.xlabel('Valores guardados en a')
plt.ylabel('Valores guardados en b')
plt.show()

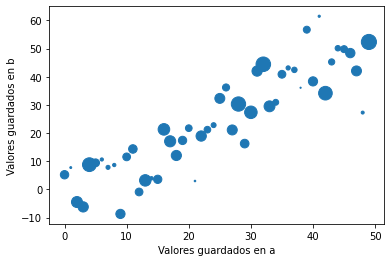
El argumento s, permite modificar el tamaño del punto según el valor dado en la variable (s=size).

Además podemos agregar una cuarta variable, por ejemplo, usemos colores:

plt.scatter('Eje x', 'Eje y',s='Tamaño',c='Color',cmap='inferno',data=data)#1
plt.xlabel('Valores guardados en a')
plt.ylabel('Valores guardados en b')
plt.show()

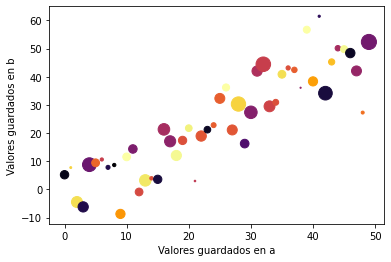
El argumento c (c de color) permite asignar un color por cada valor en la variable. El argumento cmap (colormap) es para seleccionar la paleta de colores a utilizar (para ver la gama completa de colores visite Colores).

En resumen, hemos graficado en un plano cartesiano cuatro variables, una representada por el eje horizontal, otra por el eje vertical, una más representada por el tamaño y la última representada por el color.

Gráficos para variables categóricas#

Con Matplotlib también podemos hacer gráficos de variables categóricas. Un ejemplo simple:

x=["María", "Pedro", "Juan"]
y=[10,12,8]
plt.bar(x,y)

<BarContainer object of 3 artists>

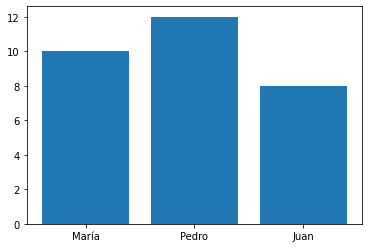
Si deseamos las barras horizontales y cambiar el color:

x=["María", "Pedro", "Juan"]
y=[10,12,8]
plt.barh(x,y,color='y')

<BarContainer object of 3 artists>

También podemos unir los puntos con líneas como hicimos al principio:

x=["María", "Pedro", "Juan"]
y=[10,12,8]
plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x7f8cab753f40>]

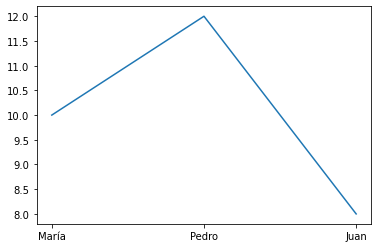
O también podríamos realizar el gráfico de dispersión para las categorías, aunque no es muy utilizado:

x=["María", "Pedro", "Juan"]
y=[10,12,8]
plt.scatter(y,x)

<matplotlib.collections.PathCollection at 0x7f8cab722ee0>

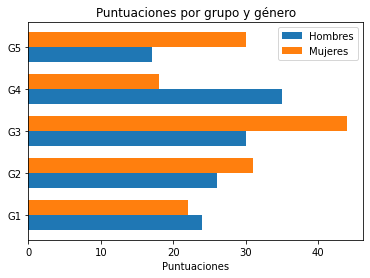
En algunas oportunidades, las variables que tratemos se prestan para realizar un gráfico de barras apilado, es decir, una barra sobre la otra separando los colores por categoría:

#Definamos los elementos con los que trabajaremos:
labels = ['G1', 'G2', 'G3', 'G4', 'G5']#Nombres de los grupos
hombres = [24, 26, 30, 35, 17]#Puntajes de los hombres
mujeres = np.array([22, 31, 44, 18, 30])#Puntajes de las mujeres
width = 0.9#Ancho de la barra

fig, ax = plt.subplots()
ax.barh(labels, mujeres, width, left=hombres,label='Mujeres')
ax.barh(labels, hombres, width, label='Hombres')
ax.set_ylabel('Puntuaciones')
ax.set_title('Puntuaciones por grupo y género')
ax.legend()

<matplotlib.legend.Legend at 0x1f5b005e7f0>

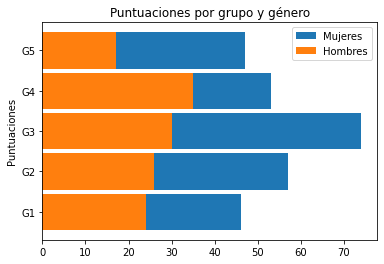
Ahora, vamos a realizar la gráfica con los datos agrupados:

x = np.arange(len(labels)) 
x

array([0, 1, 2, 3, 4])

width=0.35
x = np.arange(len(labels)) 
fig, ax = plt.subplots()
rects1 = ax.barh(x - width/2, hombres, width, label='Hombres')
rects2 = ax.barh(x+width/2, mujeres, width, label='Mujeres')
ax.set_yticks(x)
ax.set_yticklabels(labels)

ax.set_xlabel('Puntuaciones')
ax.set_title('Puntuaciones por grupo y género')
ax.legend()

<matplotlib.legend.Legend at 0x1f5afeb3280>

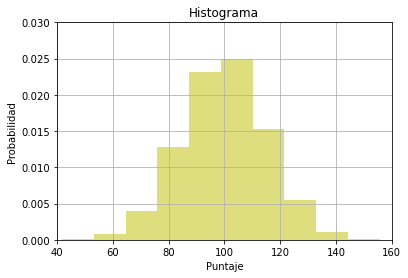
Histogramas#

Son gráficos empleados para dar un primer vistazo del comportamiento de la variable. Se hace mediante barras, y la altura de cada barra depende de la frecuencia de los valores representados:

#Generamos valores aleatorios:
mu, sigma = 100, 15
x = mu + sigma * np.random.randn(10000)

n, bins, patches = plt.hist(x, 10, density=True, facecolor='y', alpha=0.5)

plt.xlabel('Puntaje')
plt.ylabel('Probabilidad')
plt.title('Histograma')
plt.axis([40, 160, 0, 0.03])
plt.grid(True)
plt.show()

#Valor de la probabilidad
n

array([0.00014058, 0.00074686, 0.00400666, 0.0128635 , 0.02312618,
       0.02496257, 0.01526223, 0.0055531 , 0.00108953, 0.00011423])

#Valores de los extremos de las barras
bins

array([ 41.83339602,  53.21443627,  64.59547651,  75.97651676,
        87.35755701,  98.73859726, 110.11963751, 121.50067775,
       132.881718  , 144.26275825, 155.6437985 ])

#Son los contenedores que se utilizan para crear el histograma
patches

<BarContainer object of 10 artists>

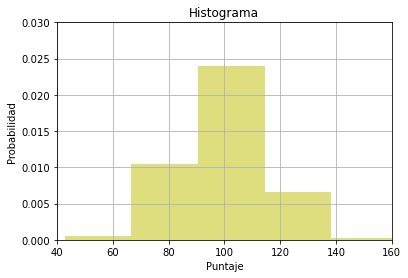
Vamos a definir una función en la que podamos controlar dos aspectos: el primero será la cantidad de barras que se graficarán y el segundo la intensidad del color:

mu, sigma = 100, 15
x = mu + sigma * np.random.randn(10000)
def histograma(n,a):
    plt.hist(x, n, density=True, facecolor='y', alpha=a)
    plt.xlabel('Puntaje')
    plt.ylabel('Probabilidad')
    plt.title('Histograma')
    plt.axis([40, 160, 0, 0.03])
    plt.grid(True)
    plt.show()
    return

histograma(5,0.5)

Ahora agregaremos los componentes de interactividad vistos en el cuaderno anterior:

import ipywidgets as widgets
from ipywidgets import interact
interact(histograma,n=widgets.IntSlider(value=30,min=1,max=50,description="Intervalos"),
         a=widgets.FloatSlider(value=0.5,min=0,max=1,description="Transparencia"))

<function __main__.histograma(n, a)>

Importaremos el paquete math para hacer un ejercicio muy interesante:

from math import sqrt
x=25
eval("sqrt(x)")

5.0

Graficador de funciones#

Haremos un graficador de funciones, cuyas variables serán: el nombre de la función (nf), los valores mínimo y máximo en el eje x (xmin, xmax) y también los valores mínimo y máximo en el eje y (ymin, ymax):

def graffun(nf,xmin,xmax,ymin,ymax):
    try:
        x = np.linspace(xmin, xmax, 100)
        y=eval(nf)
        plt.plot(x,y)
        plt.axis([xmin,xmax,ymin,ymax])
        plt.grid(True)
    except:
        print('Error!!')


interact(graffun,nf='(x-3)**2',xmin=-10,xmax=2*np.pi,ymin=-1,ymax=1)  

<function __main__.graffun(nf, xmin, xmax, ymin, ymax)>

Texto en las gráficas#

Si necesitamos introducir elementos aclaratorios en nuestras gráficas, podemos usar el comando plt.text() o el comando plt.annotate():

ax = plt.subplot(111)

t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
line, = plt.plot(t, s, lw=2)

plt.text(0.7,1.12,'Un máximo\nlocal ')#1
plt.ylim(-2, 2)
plt.show()

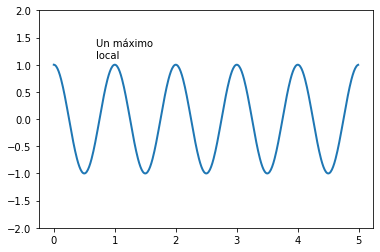
Las primeras entradas son las coordenadas del texto y la tercera es el texto que se desea agregar.

ax = plt.subplot(111)

t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
line, = plt.plot(t, s, lw=2)
#Se pueden agregar códigos Latex
plt.text(0.7,1.12,r'$\left(2\cdot\pi\cdot\frac{\pi}{2},1\right)$')
plt.title(r"Función $\cos(2\pi x)$ y un máximo local")
plt.ylim(-2, 2)
plt.show()

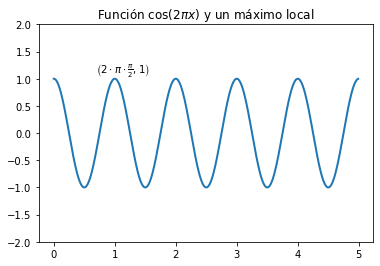
Ahora con una anotación:

ax = plt.subplot(111)

t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
line, = plt.plot(t, s, lw=2)

plt.annotate('Máximo local', xy=(1, 1), xytext=(3, 1.5),
             arrowprops=dict(edgecolor='green',facecolor='blue'),
             )#1

plt.ylim(-2, 2)
plt.show()

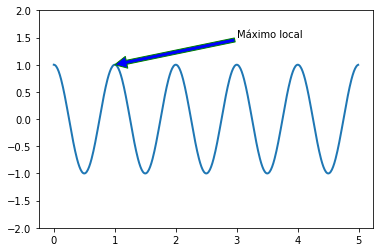
?plt.annotate

ax = plt.subplot(111)

t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
line, = plt.plot(t, s, lw=2)

plt.annotate('Máximo local', xy=(1, 1), xytext=(3, 1.5),
             arrowprops=dict(edgecolor='green',facecolor='red', shrink=0.05),)

plt.ylim(-2, 2)
plt.show()

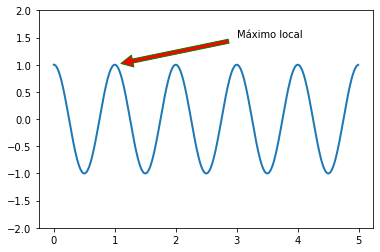
Veámos los diferentes tipos de flecha que podemos emplear en nuestras anotaciones:

def estiloflecha(l):
    ax = plt.subplot(111)

    t = np.arange(0.0, 5.0, 0.01)
    s = np.cos(2*np.pi*t)
    line, = plt.plot(t, s, lw=2)

    plt.annotate('Máximo local', xy=(1, 1), xytext=(3, 1.5),
                 arrowprops=dict(edgecolor='green',facecolor='red', arrowstyle=l),)

    plt.ylim(-2, 2)
    plt.show()
    return

interact(estiloflecha,l=['-','->','-[','|-|','-|>','fancy','simple','wedge'])

<function __main__.estiloflecha(l)>

Backends#

Al usar Jupyter nosotros estamos pidiendo que el gráfico se pueda visualizar en el entorno web en el cual se está mostrando las salidas de Python. Sin embargo, es posible visualizar estos mismos gráficos en otras interfaces gráficas más potentes y con más herramientas.

Matplotlib permite utilizar las diferentes interfáces haciendo modificación en su backend, entendiendo al backend como el motor gráfico que genera las diferentes imagenes que imaginamos.

Para modificar el backend usado en Jupyter usamos un comándo mágico %matplotlib. Veamos algunos ejemplos:

import matplotlib

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

%matplotlib notebook
ax = plt.subplot(111)
t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
line, = plt.plot(t, s, lw=2)
plt.text(0.7,1.12,'Un máximo\nlocal ')
plt.ylim(-2, 2)
#plt.show()
line

<matplotlib.lines.Line2D at 0x19a1ed1a280>

#!pip install mpld3

#Reiniciar el Kernel
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import mpld3
mpld3.enable_notebook()
ax = plt.subplot(111)
t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
line, = plt.plot(t, s, lw=2)
plt.text(0.7,1.12,'Un máximo\nlocal ')
plt.ylim(-2, 2)
plt.show()
#mpld3.show()

Programación 1

Matplotlib - Gráficos en Python

Contents

Matplotlib - Gráficos en Python#

¿Cómo funciona?#

Partes de una figura#

Ejercicio#

Figura y ejes como variables#

Diferentes tipos de gráficos#

El commando `plt.plot()`#

¿Qué estilos podemos agregar a las líneas?#

Gráficos de dispersión#

Gráficos para variables categóricas#

Histogramas#

Graficador de funciones#

Texto en las gráficas#

Backends#

Programación 1

Matplotlib - Gráficos en Python

Contents

Matplotlib - Gráficos en Python#

¿Cómo funciona?#

Partes de una figura#

Ejercicio#

Figura y ejes como variables#

Diferentes tipos de gráficos#

El commando plt.plot()#

¿Qué estilos podemos agregar a las líneas?#

Gráficos de dispersión#

Gráficos para variables categóricas#

Histogramas#

Graficador de funciones#

Texto en las gráficas#

Backends#

El commando `plt.plot()`#