Iteración y Recursión

Important

¿Cómo vamos?

Hasta el momento debemos tener claro lo siguiente:

En el siguiente código la idea es imprimir los cuatro colores, establecemos dos funciones que lo permiten. Tómate el tiempo para analizarlos y cuentanos como opera cada uno:

colores=['Amarillo','Azul','Rojo','Verde']

## Función 1
def impresion_iterativa(lista):
    for i in lista:
        print(i)

impresion_iterativa(colores)

Amarillo
Azul
Rojo
Verde

En la siguiente buscamos un resultado similar:

## Función 2
def impresion_recursiva(lista):
    if len(lista) == 1:
        lista = lista[0]
        print(lista)

    else:
        mitad = len(lista) // 2
        primera_mitad = lista[:mitad]
        segunda_mitad = lista[mitad:]

        impresion_recursiva(primera_mitad)
        impresion_recursiva(segunda_mitad)

impresion_recursiva(colores)

Amarillo
Azul
Rojo
Verde

¿Qué clase de algortimo es este?

Como podemos ver obtenemos el mismo resultado, pero en la función 2 se hace referencia a ella misma. Un ejercicio interesante es explicar que ocurre desde que inicia el algoritmo. Pensemos en un diagrama que aclare esta situación:

Observe que no importa el tamaño de la lista siempre realizará la tarea que asignamos:

Colores=['Amarillo','Azul','Rojo','Verde','Naranja','Violeta','Ocre']

impresion_recursiva(Colores)

Amarillo
Azul
Rojo
Verde
Naranja
Violeta
Ocre

Tomando como base el gráfico anterior, trata de dibujar como se imprimieron los anteriores siete colores. Veamos ahora el siguiente algorimo, usado para calcular el factorial de un número.

def factorial_iterativo(n):
    f=1
    for i in range(1,n+1):
        print(i)
        f=i*f
    return f

factorial_iterativo(5)

1
2
3
4
5

120

Comparemos con el siguiente:

def factorial_recursivo(n):
    if n==1:
        return 1
    else:
        return n*factorial_recursivo(n-1)

factorial_recursivo(5)

120

En un diagrama como el anterior explique como se está ejecutando este algoritmo.

Es un divide y venceras

Un guía adecuada para reconocer estos algoritmos recursivos es que se define un problema como simple o como una división que nos lleva a un problema más sencillo.

En terminos más formales, una función recursiva es una función definida en términos de sí misma a través de expresiones autorreferenciales. Es decir, la función continuará llamándose a sí misma y repetirá su comportamiento hasta que se cumpla alguna condición para devolver un resultado. Todas las funciones recursivas comparten una estructura común compuesta de dos partes: caso base y caso recursivo.

En los ejemplos anteriores es muy sencillo identificar este par de partes.

Estado de ejecución en funciones recursivas

En las funciones recursivas cada llamada tiene su propio contexto de ejecución, es muy importante que mientras se mantenga en el estado de recursividad se pase el estado a través de cada llamada recursiva para que el estado actual sea parte del contexto de ejecución de la llamada actual, sin embargo otra alternativa se puede plantear al mantener el estado en el ámbito global, ilustremos esta situación con los siguientes ejemplos, el objetivo es lograr la suma de los primeros diez números enteros positivos.

El siguiente mantiene el estado recursivo aplicando cada llamada recursiva como argumento:

def sum_recursive(current_number, accumulated_sum):
    # Caso Base
    # Estado final
    if current_number == 11:
        return accumulated_sum

    # Caso recursivo
    # Avanza atraves de la ejecución con llamadas recursivas
    else:
        return sum_recursive(current_number + 1, accumulated_sum + current_number)

sum_recursive(1,0)

55

La ejecución avanza de la siguiente manera:

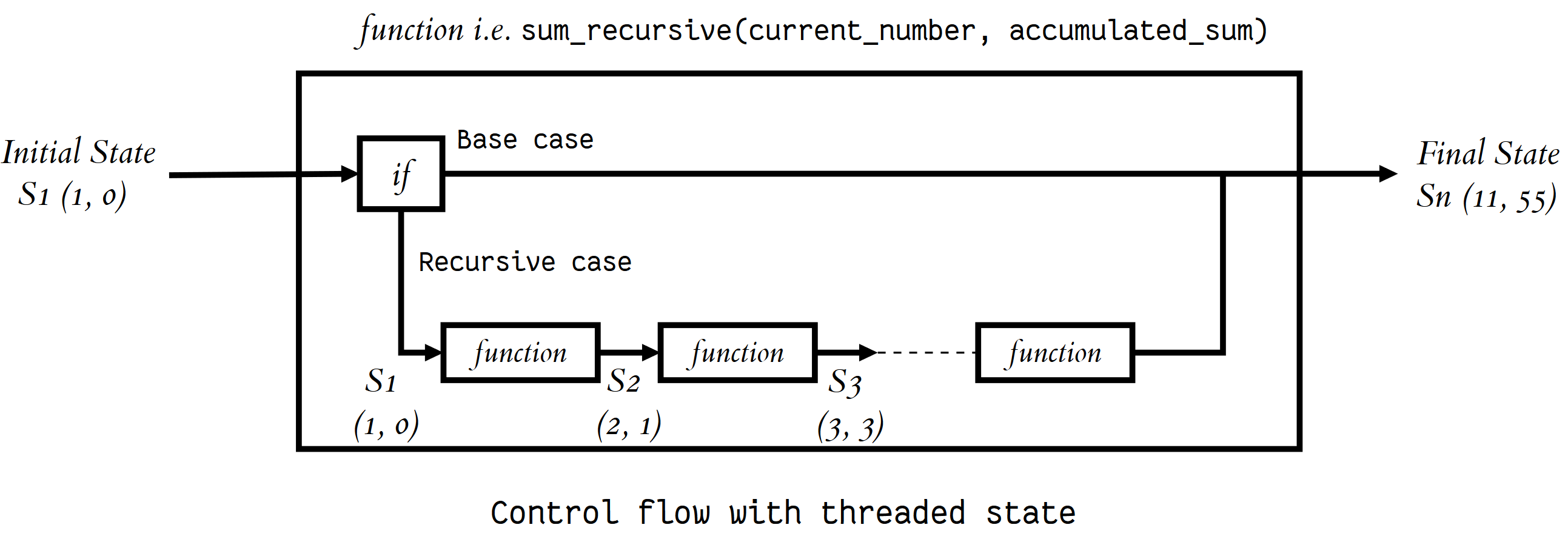
Ahora trabajemos dejando todo en el espacio de nombres global, aca current_number y accumulated_sum se mantienen como variables globales:

# Entorno global
current_number = 1
accumulated_sum = 0


def sum_recursive():
    global current_number
    global accumulated_sum
    # Caso Base
    if current_number == 11:
        return accumulated_sum
    # Caso Recursivo
    else:
        accumulated_sum = accumulated_sum + current_number
        current_number = current_number + 1
        return sum_recursive()

Estructuras de datos recursivas

Diremos que una estructura de datos es recursiva si puede definirse en términos de una versión más pequeña de sí misma.

Por ejemplo, una lista es un ejemplo de estructura de datos recursiva, es posible construir cualquier lista aplicando la siguiente función varias veces y iniciando con una lista vacía. Por ejemplo:

def elemento_adjunto(lista,elemento):
    return lista + [elemento]

elemento_adjunto(elemento_adjunto(elemento_adjunto([],1),2),3)

[1, 2, 3]

Los diccionarios, los conjuntos, los árboles admiten definición recursiva, claramente los algoritmos recursivos se montan en datos recursivos:

def suma_de_lista_recursiva(lista_inicial):
    # Caso Base
    if lista_inicial == []:
        return 0

    # Caso recursivo
    else:
        encabezado = lista_inicial[0]
        Lista_pequeña = lista_inicial[1:]
        return encabezado + suma_de_lista_recursiva(Lista_pequeña)

suma_de_lista_recursiva([])

0

suma_de_lista_recursiva([1,2,3,4])

10

Cierre

Cuando usamos herramientas recursivas estamos cambiando la forma de pensar. Es todo un arte identificar problemas que se pueden hacer pequeños y autoreferenciar. Además estamos logrando una solución elegante a prblemas que tradicionalmente se resuelven con iteraciones. Una de las características destacadas de Python, que permite la elegancia de las soluciones.